 録"
録"
nagajisの日不定記。
本日のアクセス数:0|昨日のアクセス数:0
ad
2026-02-02 [長年日記] この日を編集
[煉瓦] 長手/小口比の使い道
長手/厚比や小口/厚比で規格を推定しようという発想は形を保った構造物の煉瓦を計測する場合の方策として考えたものだった。平が見える状態で敷かれているような場合なら長手/小口の比で考えても構わない。ただしそのような場面は非常に限られているし、既知規格の長手/小口比は似通ったものになるのであまり有効な方策ではない。
のだが、ふと、発掘調査で拾い上げられ計測された煉瓦のデータをこれで活用できるんではないかと思いついた。長手や厚なら必ず3桁ミリを越えるので有効数字3桁の比を得ることができる。同一煉瓦の長手、小口を測っているので煉瓦ごとの焼き締まり度の違いもnegれる。
ちょうどいいデータを先日入手していた。市村慎太郎「旧大阪府庁舎跡出土煉瓦補遺」(『大阪文化財研究』(41)2012.9)。府庁舎跡発掘で見つかった煉瓦のうち、無刻印のものの採寸結果をリストアップしたもので(刻印のあるものは『大阪府庁舎跡』報告書に掲げられている。そこに載せられなかったものを供養した論文だ)、この寸法リストの中からオリジナルの構造である中央棟から採取されたもの65個についてExcelにしておいた。このデータはミリ2桁で厚が測られているのでそのままでは対厚比法に応用できない。そのような場合に無理に当てはめるとどうなるか試していたのだ。
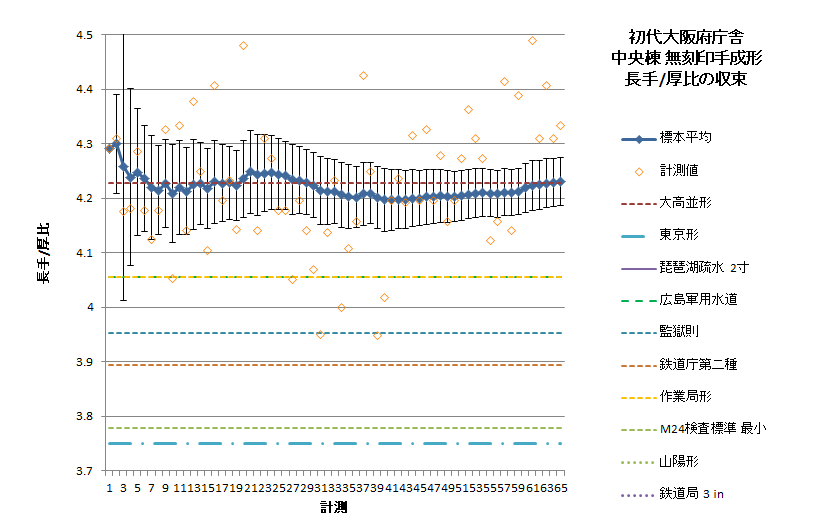
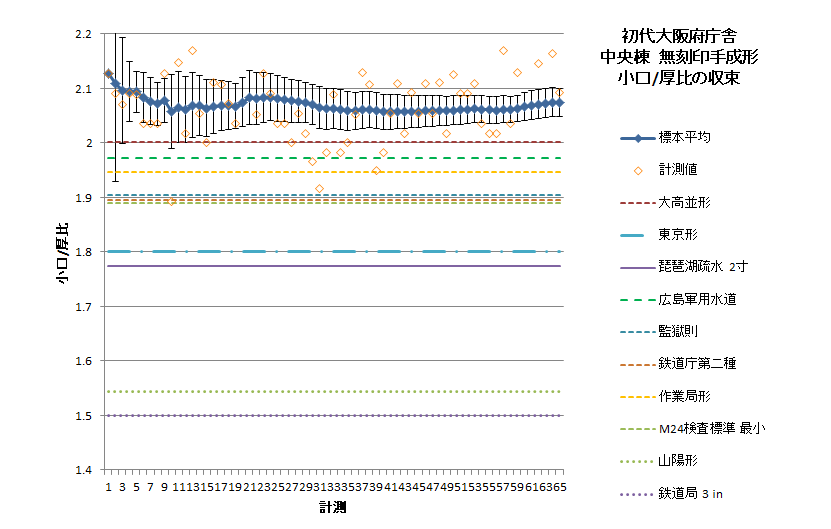
やってみるとこんな結果になる。計測数は多いものの対厚比の平均値はかなり変動するし、母平均の信頼域も大きめになって、ちょっとこれでは定値を言えない。けれどもどうだ、このデータで長手/小口比を出すと
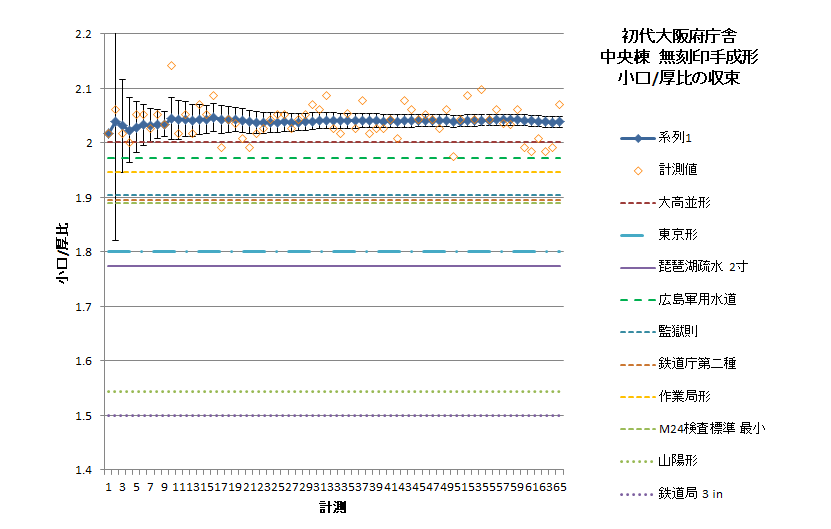
R = 2.03(8) [2.02(9), 2.04(8)]99%
非常によく収束する。
長手/厚比がよく収束するのは自分で測ってきたデータでも同様だった。有効数字4桁で計測して結果を3桁に丸めれば上の値に一致する。長手/厚比は前者4.23後者4.14でずいぶん違う値になってしまって困っていたのだった(母平均信頼区間は重なる部分が多いのだけれども)。
こんだけ精度良く絞り込めるなら長手/小口でmatrix作って尺寸なりインチなりに落とし込めるんじゃね?とほくそ笑んだのだけれども、そこがどうもうまくいかない。最も近いのは 7.65 x 3.75 寸 = 2.04 のあたりなのだが長1分・小口5厘の違いで似たような数値が現れるために(例えば7.55 x 3.70 = 2.041、 7.45 x 3.65 = 2.041)どれを狙ったものか判断できない。平均値でいえば 7.65 x 3.75 寸が一番近いけれど、結果的にそう焼けただけである可能性を払拭できない。インチに至っては3mm刻みのmatrixになるので上記範囲に捉えられる数字すらなかった。対厚比法がうまく行っているのは長手・小口・厚をセットで捉えられているからだ。長手/小口比だけでは未知変数3の方程式を2連立で解こうとするようなもの。
ひとつ言えるのは、平の矩形は長手や小口よりも等方的に焼き縮んでいて、元の型枠の大きさをよく保持しているようだということ。厚の計測はどうしても変動要素が多すぎる。裏平の凹線がある側を測った場合と反対側を測った場合では煉瓦表面で測れる厚が異なる可能性が高い(想像しているような手順で凹線がつくのであれば長手縁が器具で押されたり反対側の角が台に強くあたって歪んでしまう可能性がある)。同じ面内でも場所によって焼き締まり方が異なるために厚も異なる。そうして厚の変動が対厚比に最も大きな影響を及ぼす。要するに構造物表面で厚を正確に測ることは難しい。
それから、既報の論文にある採寸結果からさらなる情報を引き出したい時にも使える。対厚比で強引に数値を出すよりも長手/小口比のほうが精確な数字を得られるのは上記実験からも明らかで、問題はその数字が役に立たない時があるという点だ。この値と強引に出した対厚比とを組合せればあるいは判断できるかも知れないが……そこはまだよく考察していない。
長手/厚比を小口/厚比で割れば長手/小口比を得られるので、有効数字4桁で測ったデータから長手/小口比を得ることはできるけれども、収束していくさまを見ることはできず、母平均信頼区間も擬似的にしか出せない(はず)。そうしてその信頼区間はどちらかの対厚比の信頼区間の大きい方よりもさらに大きくなるんじゃないか。試しにやってみたがやはり美味くなかった。