録"

[煉瓦] 掟破りの取捨選択

煉瓦規格を対厚比で推定しようという試みを検証しているのだが、前提としている仮定にかなり無理があることがわかってきた。素地の大きさはどれも一緒で、その焼き縮みの比率が各煉瓦で違うだけなのではないかと考え、その比を取ることで焼き縮み率の影響を取り除こうというのが対厚比法のキモなのだけれども、各個測定した20数点の長手と厚の寸法について相関係数を取ってみるとよほどうまくいった場合でも0.6くらいがせいぜいで、ひどい時には0.01とかいう値になる。長手と厚の間に全く相関関係がないということになり、長手と厚の比が云々なんて意味がなくなってしまう。

理由はいろいろ考えられる。そもそも煉瓦が等方的に焼き縮んでいない、あるいは乾燥時に等方的に収縮していない可能性。等方的に焼き縮んでいないものが20数個の計測の中に混じっているのは間違いない。長手だけとか小口だけとかが焼き縮んだようなもの、長手小口が変形したものが随分入っているのではないか。これは関西の例ではないが、浜名橋梁の井筒を調べた時に東京煉瓦の○T印刻印のひしゃげたものが多くあったのを思い出した。素地に打刻した時には真円だったはずだが（それがうまく焼けたら上写真のようになる）、焼く時に長手より小口のほうが強く焼き縮んだか整形時に小口が圧縮されるような修正が加えられた結果、印が歪んで縦長になってしまったものと思う（下写真）。

この変形の原因は、おそらく、焼成時の積み方が大きく影響している。スタックの下の方の煉瓦はそれより上の煉瓦の重さを受けるわけなので、小端立てにして積んでいれば小口方向に潰れやすいものと思う。あるいは長手方向が他の煉瓦によって拘束されるため焼き縮みにくいのかも知れない。同じ窯の製品でも長手が±2分＝6mm、最大最小の差が1.2cmも変動するというのはそういうところから来ていると思う。（下写真は中川煉瓦で実際に採用されていた詰め方。小口を小端立てて井桁に組む）

あるいは取り板に取ったあとの乾燥の作業でひっくり返したり移したりする作業工程で大きく変形してしまうことも考えられる。型枠から抜いた直後は型枠の寸法比を保っているだろうが、それが歪んで再整形したとき、元の型枠の寸法比の通りに整形されるとは限らない。目分量でだいたい同じにされれば１分変わることも容易に想像される。そういう〝歪んだ煉瓦〟が無造作に混じっているから相関が低い結果になるんじゃなかろうか。

だとすれば採寸して比を取ること自体無意味なことになってしまう。かといってこれまでの検証を全部ポイする気にもなれない。私は往生際が悪いのである。

構造物に使われている煉瓦の中に規格の比から外れた〝歪んだ煉瓦〟が混じっているものだとすれば、そういうやつまで測る必要はなく、それらも含めて平均値なり不偏分散なりを算出しても真から外れるばかりだろう。明らかに歪んだものは測定時に排除するようにしてきたけれども、それをもっと積極的にやってもいいんじゃないか。計測した数値のなかで歪んでいると判断されるものを省いてもいいんじゃないか。都合のよい数値を恣意的に選んでいることになってしまうが、そうでもしないと煉瓦の寸法は理解できないのではないか。

じゃあ具体的にどうするか。理論は簡単。要するに長手対厚の比が似通ったものを選べばいいわけである。その「似通った」の判定は長手・厚のデータセットの相関係数で判断すればいいのではないか。20数個計測したもののなかから相関係数が最大となる10数個を使って比を出すなり寸法絶対値を出すなりすればよい。そう考え、例えば₂₀C₁₀の組み合わせについて総当たりで相関係数を出し、それが最も大きくなる組み合わせを見つけ出すようなプログラムをでっち上げて試してみた。

例えば京都大阪間の山端暗渠。これは比較的正確に測れたと思っている暗渠で（目地が抜けつつあるのでモルタル被りなしの煉瓦の実寸を計測できている）、それでも長手/厚は0.49、小口/厚は0.60という相関係数。このなかから相関係数最大になるような組み合わせを探させると

こうなる。どちらも0.9+という驚異的な？相関係数が得られ（点数が少なくなった時点で相関係数は上がるんだろうが）、その組み合わせで算出した長手/厚比と小口/厚比の組み合わせは同じ路線の他の構造物のとよく一致してくれる。4.05＜μ_長手/厚＜4.17、1.96＜μ_小口/厚＜2.02。京都大阪間の煉瓦はどれも4.10前後、2.00前後に落ち着く。

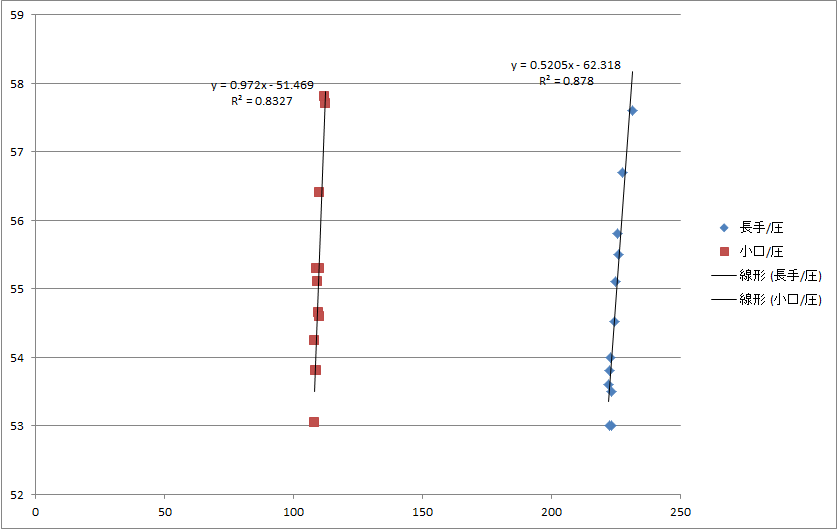
これを田中源太郎の楽々荘の煉瓦でやると、20数個の平均値で計算した時よりはるかに監獄則類似になるのだった。龍谷大学旧守衛舎は₃₀C₁₂がメモリ不足で計算できなかったが、適当に22に減らしたうえで計算し直してやはり長手/厚比が監獄則煉瓦に近づいた。京都の煉瓦が監獄則煉瓦の比率であることが多いのはまことに示唆的だと思う。

問題は、こんな恣意的な計算が許されるのかっちゅう話や。話はどんどん大きく怪しくなっていく方向へ転がっていく石の苔。

メモリ不足を解消するにはｎCrのfunctionのなかで相関係数の算出と最大値かどうかのチェックをすればよさげ。足らんくなるのはnCrの関数のなかでなので不要なやつはさっさと消していけば解決するんじゃなかろうか。ｎCrを全部配列で返して改めてforeachしてたらそりゃメモリ足らん。